make.polyhedron

make.polyhedron will modify an initial topobathymetric surface by adding or subtractracting a polyhedron based on user-defined planes. The following is typical usage for make.polyhedron.

1. Prepare a topography file as a geotif.

2. Prepare or obtain a polygon shapefile indicating where the polyhedron should be applied. Ensure that the geotif and shapefile have the same coordinate system.

3. Determine a list of dictionaries, each specifying a plane of the desired polyhedron.

4. Run make.polyhedron to modify the topobathymetry file. Inspect the output and adjust any input parameters as needed.

5. 4. Using these files, set up a D-Claw simulation to run and analyze. digger will not do this for you.

A code snippet that uses make.polyhedron may be found in the file digger/examples/pre-run/black_lake/make_polyhedron_black_lake_example.py. In this example, a polyhedron is removed from above Black Lake.

"""An example of using digger.make.polyhedron.

This example uses Black Lake topography and provides an example of using
digger.make.polyhedron.
"""

from digger import make

# Run digger.make.polyhedron

black_lake = make.polyhedron(
    topo_path="../../../data/black_lake_dem.tif",
    mask_path="../../../data/black_lake_poly_ext.shp",
    planes=[
        {"xyz": (419857.58, 5129669.36, -5), "dip_dir": 360, "dip": 60},
        {"xyz": (419857.58, 5129669.36, -5), "dip_dir": 120, "dip": 60},
        {"xyz": (419857.58, 5129669.36, -5), "dip_dir": 240, "dip": 60},
    ],
    mask_to_water=False,
    sense="subtract",
    write_tif=True,
    write_tt3=False,
    b_prefix="b_polyhedron",
    q1_prefix="q1_polyhedron",
    eta_prefix="eta_polyhedron",
    fig_path="polyhedron.png",
)

After this code runs, it will produce geotif and topotype3 files that specify the modified topobathymetry.

It will also create diagnostic figures.

The standard diagnostic figure from make.polyhedron

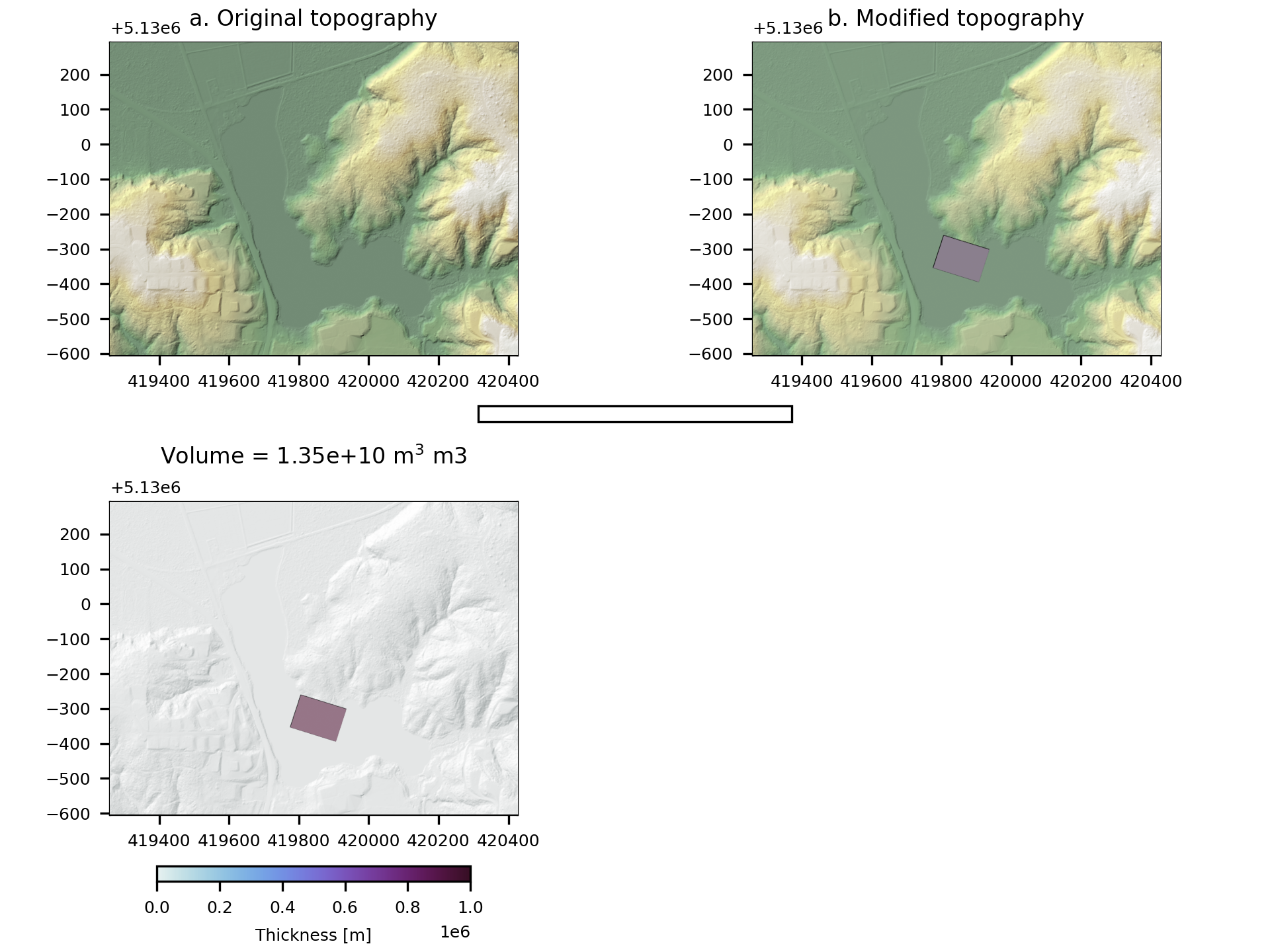
Fig. 8 An example of the diagnostic output provided by digger.make.polyhedron.